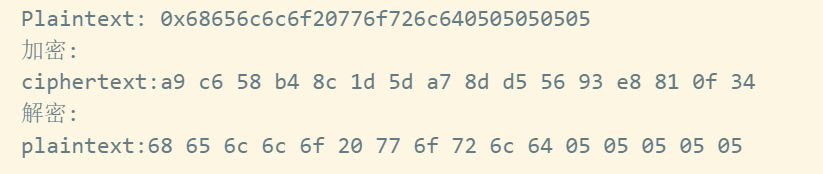
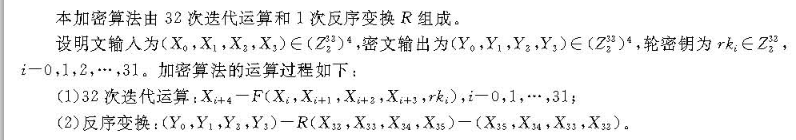1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
|
S_BOX = [0xD6, 0x90, 0xE9, 0xFE, 0xCC, 0xE1, 0x3D, 0xB7, 0x16, 0xB6, 0x14, 0xC2, 0x28, 0xFB, 0x2C, 0x05,
0x2B, 0x67, 0x9A, 0x76, 0x2A, 0xBE, 0x04, 0xC3, 0xAA, 0x44, 0x13, 0x26, 0x49, 0x86, 0x06, 0x99,
0x9C, 0x42, 0x50, 0xF4, 0x91, 0xEF, 0x98, 0x7A, 0x33, 0x54, 0x0B, 0x43, 0xED, 0xCF, 0xAC, 0x62,
0xE4, 0xB3, 0x1C, 0xA9, 0xC9, 0x08, 0xE8, 0x95, 0x80, 0xDF, 0x94, 0xFA, 0x75, 0x8F, 0x3F, 0xA6,
0x47, 0x07, 0xA7, 0xFC, 0xF3, 0x73, 0x17, 0xBA, 0x83, 0x59, 0x3C, 0x19, 0xE6, 0x85, 0x4F, 0xA8,
0x68, 0x6B, 0x81, 0xB2, 0x71, 0x64, 0xDA, 0x8B, 0xF8, 0xEB, 0x0F, 0x4B, 0x70, 0x56, 0x9D, 0x35,
0x1E, 0x24, 0x0E, 0x5E, 0x63, 0x58, 0xD1, 0xA2, 0x25, 0x22, 0x7C, 0x3B, 0x01, 0x21, 0x78, 0x87,
0xD4, 0x00, 0x46, 0x57, 0x9F, 0xD3, 0x27, 0x52, 0x4C, 0x36, 0x02, 0xE7, 0xA0, 0xC4, 0xC8, 0x9E,
0xEA, 0xBF, 0x8A, 0xD2, 0x40, 0xC7, 0x38, 0xB5, 0xA3, 0xF7, 0xF2, 0xCE, 0xF9, 0x61, 0x15, 0xA1,
0xE0, 0xAE, 0x5D, 0xA4, 0x9B, 0x34, 0x1A, 0x55, 0xAD, 0x93, 0x32, 0x30, 0xF5, 0x8C, 0xB1, 0xE3,
0x1D, 0xF6, 0xE2, 0x2E, 0x82, 0x66, 0xCA, 0x60, 0xC0, 0x29, 0x23, 0xAB, 0x0D, 0x53, 0x4E, 0x6F,
0xD5, 0xDB, 0x37, 0x45, 0xDE, 0xFD, 0x8E, 0x2F, 0x03, 0xFF, 0x6A, 0x72, 0x6D, 0x6C, 0x5B, 0x51,
0x8D, 0x1B, 0xAF, 0x92, 0xBB, 0xDD, 0xBC, 0x7F, 0x11, 0xD9, 0x5C, 0x41, 0x1F, 0x10, 0x5A, 0xD8,
0x0A, 0xC1, 0x31, 0x88, 0xA5, 0xCD, 0x7B, 0xBD, 0x2D, 0x74, 0xD0, 0x12, 0xB8, 0xE5, 0xB4, 0xB0,
0x89, 0x69, 0x97, 0x4A, 0x0C, 0x96, 0x77, 0x7E, 0x65, 0xB9, 0xF1, 0x09, 0xC5, 0x6E, 0xC6, 0x84,
0x18, 0xF0, 0x7D, 0xEC, 0x3A, 0xDC, 0x4D, 0x20, 0x79, 0xEE, 0x5F, 0x3E, 0xD7, 0xCB, 0x39, 0x48
]
FK = [0xa3b1bac6, 0x56aa3350, 0x677d9197, 0xb27022dc]
CK = [
0x00070e15, 0x1c232a31, 0x383f464d, 0x545b6269,
0x70777e85, 0x8c939aa1, 0xa8afb6bd, 0xc4cbd2d9,
0xe0e7eef5, 0xfc030a11, 0x181f262d, 0x343b4249,
0x50575e65, 0x6c737a81, 0x888f969d, 0xa4abb2b9,
0xc0c7ced5, 0xdce3eaf1, 0xf8ff060d, 0x141b2229,
0x30373e45, 0x4c535a61, 0x686f767d, 0x848b9299,
0xa0a7aeb5, 0xbcc3cad1, 0xd8dfe6ed, 0xf4fb0209,
0x10171e25, 0x2c333a41, 0x484f565d, 0x646b7279
]
def wd_to_byte(wd, bys):
bys.extend([(wd >> i) & 0xff for i in range(24, -1, -8)])
def bys_to_wd(bys):
ret = 0
for i in range(4):
bits = 24 - i * 8
ret |= (bys[i] << bits)
return ret
def s_box(wd):
"""
进行非线性变换,查S盒
:param wd: 输入一个32bits字
:return: 返回一个32bits字 ->int
"""
ret = []
for i in range(0, 4):
byte = (wd >> (24 - i * 8)) & 0xff
row = byte >> 4
col = byte & 0x0f
index = (row * 16 + col)
ret.append(S_BOX[index])
return bys_to_wd(ret)
def rotate_left(wd, bit):
"""
:param wd: 待移位的字
:param bit: 循环左移位数
:return:
"""
return (wd << bit & 0xffffffff) | (wd >> (32 - bit))
def Linear_transformation(wd):
"""
进行线性变换L
:param wd: 32bits输入
"""
return wd ^ rotate_left(wd, 2) ^ rotate_left(wd, 10) ^ rotate_left(wd, 18) ^ rotate_left(wd, 24)
def Tx(k1, k2, k3, ck):
"""
密钥扩展算法的合成变换
"""
xor = k1 ^ k2 ^ k3 ^ ck
t = s_box(k1 ^ k2 ^ k3 ^ ck)
return t ^ rotate_left(t, 13) ^ rotate_left(t, 23)
def T(x1, x2, x3, rk):
"""
加密算法轮函数的合成变换
"""
t = x1 ^ x2 ^ x3 ^ rk
t = s_box(t)
return t ^ rotate_left(t, 2) ^ rotate_left(t, 10) ^ rotate_left(t, 18) ^ rotate_left(t, 24)
def key_extend(main_key):
MK = [(main_key >> (128 - (i + 1) * 32)) & 0xffffffff for i in range(4)]
keys = [FK[i] ^ MK[i] for i in range(4)]
RK = []
for i in range(32):
t = Tx(keys[i + 1], keys[i + 2], keys[i + 3], CK[i])
k = keys[i] ^ t
keys.append(k)
RK.append(k)
return RK
def R(x0, x1, x2, x3):
x0 &= 0xffffffff
x1 &= 0xffffffff
x2 &= 0xffffffff
x3 &= 0xffffffff
s = f"{x3:08x}{x2:08x}{x1:08x}{x0:08x}"
return s
|